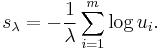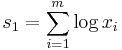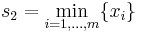Well-behaved statistic
A well-behaved statistic is a term sometimes used in the theory of statistics to describe part of a procedure. This usage is broadly similar to the use of well-behaved in more general mathematics. It is essentially an assumption about the formulation of an estimation procedure (which entails the specification of an estimator or statistic) that is used to avoid giving extensive details about what conditions need to hold. In particular it means that the statistic is not an unusual one in the context being studied. Due to this, the meaning attributed to well-behaved statistic may vary from context to context.
The present article is mainly concerned with the context of data mining procedures applied to statistical inference and, in particular, to the group of computationally intensive procedure that have been called algorithmic inference.
Contents |
Algorithmic inference
In algorithmic inference, the property of a statistic that is of most relevance is the pivoting step which allows to transference of probability-considerations from the sample distribution to the distribution of the parameters representing the population distribution in such a way that the conclusion of this statistical inference step is compatible with the sample actually observed.
By default, capital letters (such as U, X) will denote random variables and small letters (u, x) their corresponding realizations and with gothic letters (such as 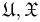 ) the domain where the variable takes specifications. Facing a sample
) the domain where the variable takes specifications. Facing a sample 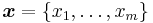 , given a sampling mechanism
, given a sampling mechanism 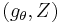 , with
, with  scalar, for the random variable X, we have
scalar, for the random variable X, we have
The sampling mechanism 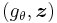 , of the statistic s, as a function ? of
, of the statistic s, as a function ? of 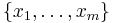 with specifications in
with specifications in 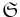 , has an explaining function defined by the master equation:
, has an explaining function defined by the master equation:
for suitable seeds 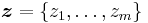 and parameter ?
and parameter ?
Well-behaved
In order to derive the distribution law of the parameter T, compatible with 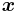 , the statistic must obey some technical properties. Namely, a statistic s is said to be well-behaved if it satisfies the following three statements:
, the statistic must obey some technical properties. Namely, a statistic s is said to be well-behaved if it satisfies the following three statements:
- monotonicity. A uniformly monotone relation exists between s and ? for any fixed seed
 – so as to have a unique solution of (1);
– so as to have a unique solution of (1); - well-defined. On each observed s the statistic is well defined for every value of ?, i.e. any sample specification
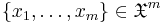 such that
such that 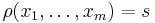 has a probability density different from 0 – so as to avoid considering a non-surjective mapping from
has a probability density different from 0 – so as to avoid considering a non-surjective mapping from 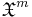 to
to 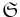 , i.e. associating via
, i.e. associating via  to a sample
to a sample 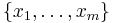 a ? that could not generate the sample itself;
a ? that could not generate the sample itself; - local sufficiency.
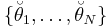 constitutes a true T sample for the observed s, so that the same probability distribution can be attributed to each sampled value. Now,
constitutes a true T sample for the observed s, so that the same probability distribution can be attributed to each sampled value. Now, 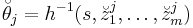 is a solution of (1) with the seed
is a solution of (1) with the seed 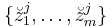 . Since the seeds are equally distributed, the sole caveat comes from their independence or, conversely from their dependence on ? itself. This check can be restricted to seeds involved by s, i.e. this drawback can be avoided by requiring that the distribution of
. Since the seeds are equally distributed, the sole caveat comes from their independence or, conversely from their dependence on ? itself. This check can be restricted to seeds involved by s, i.e. this drawback can be avoided by requiring that the distribution of 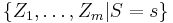 is independent of ?. An easy way to check this property is by mapping seed specifications into
is independent of ?. An easy way to check this property is by mapping seed specifications into  s specifications. The mapping of course depends on ?, but the distribution of
s specifications. The mapping of course depends on ?, but the distribution of 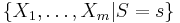 will not depend on ?, if the above seed independence holds – a condition that looks like a local sufficiency of the statistic S.
will not depend on ?, if the above seed independence holds – a condition that looks like a local sufficiency of the statistic S.
Example
For instance, for both the Bernoulli distribution with parameter p and the exponential distribution with parameter ? the statistic 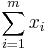 is well-behaved. The satisfaction of the above three properties is straightforward when looking at both explaining functions:
is well-behaved. The satisfaction of the above three properties is straightforward when looking at both explaining functions: 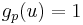 if
if 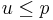 , 0 otherwise in the case of the Bernoulli random variable, and
, 0 otherwise in the case of the Bernoulli random variable, and 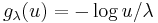 for the Exponential random variable, giving rise to statistics
for the Exponential random variable, giving rise to statistics
and
Vice versa, in the case of X following a continuous uniform distribution on ![[0,A]](/2012-wikipedia_en_all_nopic_01_2012/I/0c9ad80871fb8909dbd6499da2f961c2.png) the same statistics do not meet the second requirement. For instance, the observed sample
the same statistics do not meet the second requirement. For instance, the observed sample 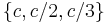 gives
gives 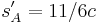 . But the explaining function of this X is
. But the explaining function of this X is 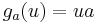 . Hence a master equation
. Hence a master equation 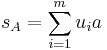 would produce with a U sample
would produce with a U sample 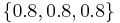 and a solution
and a solution 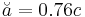 . This conflicts with the observed sample since the first observed value should result greater than the right extreme of the X range. The statistic
. This conflicts with the observed sample since the first observed value should result greater than the right extreme of the X range. The statistic 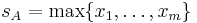 is well-behaved in this case.
is well-behaved in this case.
Analogously, for a random variable X following the Pareto distribution with parameters K and A (see Pareto example for more detail of this case),
and
can be used as joint statistics for these parameters.
As a general statement that holds under weak conditions, sufficient statistics are well-behaved with respect to the related parameters. The table below gives sufficient / Well-behaved statistics for the parameters of some of the most commonly used probability distributions.
| Distribution | Definition of density function | Sufficient/Well-behaved statistic |
|---|---|---|
| Uniform discrete | 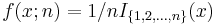 |
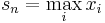 |
| Bernoulli | 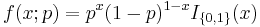 |
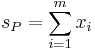 |
| Binomial | 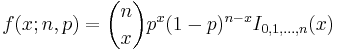 |
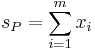 |
| Geometric | 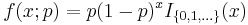 |
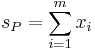 |
| Poisson | 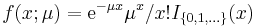 |
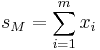 |
| Uniform continuous | ![f(x;a,b)=1/(b-a) I_{[a,b]}(x)](/2012-wikipedia_en_all_nopic_01_2012/I/bdae7ad6b981eeb7c7fea950e51c5ffb.png) |
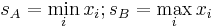 |
| Negative exponential | ![f(x;\lambda)=\lambda \mathrm e^{-\lambda x} I_{[0,\infty]}(x)](/2012-wikipedia_en_all_nopic_01_2012/I/1a1847d3a5402c6cf76b7b3603c3e4ef.png) |
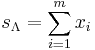 |
| Pareto | ![f(x;a, k)= \frac{a}{k}\left(\frac{x}{k}\right)^{-a -1} I_{[k,\infty]}(x)](/2012-wikipedia_en_all_nopic_01_2012/I/6a71d91ace1791e51b47f79fe4ff7a64.png) |
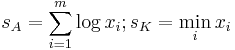 |
| Gaussian | 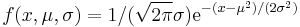 |
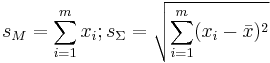 |
| Gamma | ![f(x;r,\lambda)= \lambda/\Gamma(r) (\lambda x)^{r-1} \mathrm e^{-\lambda x} I_{[0,\infty]}(x)](/2012-wikipedia_en_all_nopic_01_2012/I/04a1a2eb07f8a05ea7bdf80a4c20058f.png) |
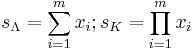 |
Notes
References
- Apolloni, B; Bassis, S., Malchiodi, D., Witold, P. (2008). The Puzzle of Granular Computing. Studies in Computational Intelligence. 138. Berlin: Springer.
- Bahadur, R. R.; Lehmann, E. L. (1955). "Two comments on Sufficiency and Statistical Decision Functions". Annals of Mathematical Statistics 26: 139–142. doi:10.1214/aoms/1177728604.
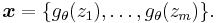
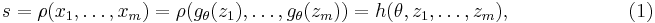
![s_p=\sum_{i=1}^m I_{[0,p]}(u_i)](/2012-wikipedia_en_all_nopic_01_2012/I/8e12b4f333bcce76597de30b518213c2.png)